Cycle 2
Programme de Mathématiques en cycle 2
BO du 31 octobre 2024 : nouveaux programmes de français et mathématiques pour les cycles 2, applicables à la rentrée 2025
En 2 min ⚡
e programme de mathématiques du cycle 2 (CP, CE1, CE2) pose les fondations solides de la numération et du calcul. Les élèves apprennent à maîtriser les nombres jusqu'à 10 000, mémorisent leurs tables d'addition et de multiplication, et développent des stratégies de calcul mental efficaces. Ils découvrent les fractions comme parts d'un tout, manipulent l'argent pour comprendre les nombres décimaux, et résolvent des problèmes de plus en plus complexes en plusieurs étapes.
En géométrie, ils construisent des figures précises avec règle, équerre et compas, calculent des périmètres et explorent la symétrie. Pour les mesures, ils jonglent entre mètres, grammes et litres, lisent l'heure et calculent des durées. L'objectif : que chaque élève sorte du CE2 avec des automatismes de calcul solides et une boîte à outils mathématiques bien remplie pour aborder sereinement le cycle 3. Tout repose sur un entraînement quotidien, des manipulations concrètes et la résolution régulière de problèmes pour donner du sens aux apprentissages.
Nombres, calcul et résolution de problèmes
- Les nombres entiers
38 objectifs
- CP Comparer et dénombrer des collections en les organisant
- CP Construire des collections de cardinal donné
- CP Connaitre la suite écrite et la suite orale des nombres jusqu'à cent
- CP Connaitre et utiliser diverses représentations d'un nombre et passer de l'une à l'autre
- CP Connaitre la valeur des chiffres en fonction de leur position (unités, dizaines)
- CP Comparer, encadrer, intercaler des nombres entiers en utilisant les symboles =, < et >
- CP Ordonner des nombres dans l'ordre croissant ou décroissant
- CP Savoir placer des nombres sur une demi-droite graduée de un en un
- CP Connaitre les nombres ordinaux jusqu'à «vingtième»
- CP Comprendre et utiliser les nombres ordinaux
- CP Repérer un rang ou une position dans une file orientée ou dans une liste d'objets ou de personnes
- CP Faire le lien entre le rang d'un objet dans une liste et le nombre d'éléments qui le précèdent
- CP Utiliser les nombres ordinaux dans le cadre de l'étude de suites de symboles, de formes, de lettres ou de nombres
- CE1 Dénombrer des collections en les organisant
- CE1 Construire des collections de cardinal donné
- CE1 Connaitre et utiliser la relation entre unités et dizaines, entre dizaines et centaines, entre unités et centaines
- CE1 Connaitre la suite écrite et la suite orale des nombres jusqu'à mille
- CE1 Connaitre et utiliser diverses représentations d'un nombre et passer de l'une à l'autre
- CE1 Connaitre la valeur des chiffres en fonction de leur position dans un nombre
- CE1 Comparer, encadrer, intercaler des nombres entiers en utilisant les symboles (=, <, >)
- CE1 Ordonner des nombres dans l'ordre croissant ou décroissant
- CE1 Comprendre et savoir utiliser les expressions «égal à», «supérieur à», «inférieur à», «compris entre … et …»
- CE1 Savoir placer des nombres sur une demi-droite graduée
- CE1 Connaitre les nombres ordinaux jusqu'à cent
- CE1 Comprendre et utiliser les nombres ordinaux
- CE1 Repérer un rang ou une position dans une file orientée ou dans une liste d'objets ou de personnes
- CE1 Faire le lien entre le rang d'un objet dans une liste et le nombre d'éléments qui le précèdent
- CE1 Utiliser les nombres ordinaux dans le cadre de suite de symboles, de lettres ou de nombres
- CE2 Dénombrer des collections
- CE2 Construire des collections de cardinal donné
- CE2 Connaitre et utiliser les relations entre les unités de numération
- CE2 Connaitre la suite écrite et la suite orale des nombres jusqu'à dix-mille
- CE2 Connaitre et utiliser diverses représentations d'un nombre et passer de l'une à l'autre
- CE2 Connaitre la valeur des chiffres en fonction de leur position dans un nombre
- CE2 Comparer, encadrer, intercaler des nombres entiers en utilisant les symboles (=, <, >)
- CE2 Ordonner des nombres dans l'ordre croissant ou décroissant
- CE2 Comprendre et savoir utiliser les expressions «égal à», «supérieur à», «inférieur à», «compris entre … et …»
- CE2 Savoir placer des nombres sur une demi-droite graduée
-
- Les fractions
10 objectifs
- CE1 Savoir interpréter, représenter, écrire et lire les fractions 1/2, 1/3, 1/4, 1/5, 1/6, 1/8 et 1/10
- CE1 Savoir interpréter, représenter, écrire et lire des fractions inférieures ou égales à 1
- CE1 Connaitre et utiliser les mots «dénominateur» et «numérateur»
- CE1 Comparer des fractions ayant le même dénominateur
- CE1 Comparer des fractions dont le numérateur est 1
- CE1 Additionner et soustraire des fractions de même dénominateur
- CE2 Savoir établir des égalités de fractions inférieures ou égales à 1
- CE2 Partager une unité de longueur en fractions d'unité et mesurer des longueurs non entières par rapport à cette unité
- CE2 Comparer des fractions inférieures à 1
- CE2 Additionner et soustraire des fractions
-
- Les quatre opérations
13 objectifs
- CP Comprendre le sens de l'addition et de la soustraction
- CP Comprendre et utiliser les symboles «+», «-» et «=»
- CP Poser et effectuer des additions en colonnes
- CP Comprendre le sens de la multiplication
- CE1 Poser et effectuer des additions et des soustractions en colonnes
- CE1 Comprendre et utiliser le symbole «×»
- CE1 Comprendre et savoir que la multiplication est commutative
- CE1 Connaitre la notion de parité d'un nombre
- CE2 Comprendre et utiliser les mots «terme», «somme» et «différence»
- CE2 Poser et effectuer des additions et des soustractions en colonnes
- CE2 Comprendre et utiliser les mots «facteur», «produit» et «multiple»
- CE2 Comprendre le sens de la division et utiliser le symbole «÷»
- CE2 Poser et effectuer des multiplications d'un nombre à deux ou trois chiffres par un nombre à un ou deux chiffres
-
- Le calcul mental
30 objectifs
- CP Connaitre dans les deux sens les tables d'addition
- CP Connaitre les doubles et les moitiés de nombres usuels
- CP Ajouter ou soustraire 1 ou 2 à un nombre
- CP Ajouter ou soustraire 10 à un nombre
- CP Ajouter ou soustraire 20, 30, 40, 50, 60, 70, 80 ou 90 à un nombre
- CP Trouver le complément d'un nombre à la dizaine supérieure
- CP Ajouter un nombre inférieur à 9 à un nombre
- CP Ajouter 9 à un nombre
- CP Ajouter deux nombres inférieurs à 100
- CP Déterminer la moitié d'un nombre pair
- CP Soustraire un nombre inférieur à 10 à un nombre entier de dizaines
- CE1 Connaitre dans les deux sens les tables d'addition
- CE1 Connaitre dans les deux sens les tables de multiplication
- CE1 Connaitre des faits multiplicatifs usuels
- CE1 Ajouter ou soustraire un nombre entier de dizaines à un nombre. Ajouter ou soustraire un nombre entier de centaines à un nombre.
- CE1 Multiplier par 10 un nombre inférieur à 100
- CE1 Ajouter 9, 19 ou 29 à un nombre
- CE1 Soustraire 9 à un nombre
- CE1 Soustraire un nombre inférieur à 9 à un nombre
- CE1 Déterminer la moitié d'un nombre pair
- CE1 Calculer le produit d'un nombre compris entre 11 et 19 par un nombre inférieur à 10 en décomposant le plus grand des deux facteurs en la somme de deux nombres (propriété de distributivité de la multiplication par rapport à l'addition)
- CE2 Connaitre dans les deux sens les tables d'addition
- CE2 Connaitre dans les deux sens les tables de multiplication
- CE2 Connaitre des faits multiplicatifs usuels
- CE2 Multiplier un nombre entier par 10 ou 100
- CE2 Ajouter 8, 9, 18, 19, 28, 29, 38 ou 39 à un nombre
- CE2 Soustraire 9, 19, 29 ou 39 à un nombre
- CE2 Multiplier un nombre entier par 4 ou par 8
- CE2 Multiplier un nombre inférieur à 10 par un nombre entier de dizaines
- CE2 Calculer le produit d'un nombre compris entre 11 et 99 par un nombre inférieur à 10 en décomposant le plus grand des deux facteurs en la somme de deux nombres (propriété de distributivité de la multiplication par rapport à l'addition)
-
- La résolution de problèmes
14 objectifs
- CP Résoudre des problèmes additifs en une étape du type parties-tout
- CP Résoudre des problèmes additifs en deux étapes (champ numérique inférieur ou égal à 30)
- CP Résoudre des problèmes multiplicatifs en une étape (champ numérique inférieur ou égal à 30)
- CE1 Résoudre des problèmes additifs en une étape de type parties-tout
- CE1 Résoudre des problèmes additifs de comparaison en une étape
- CE1 Résoudre des problèmes additifs en deux étapes
- CE1 Résoudre des problèmes multiplicatifs en une étape
- CE1 Résoudre des problèmes mixtes en deux étapes (une étape additive et une étape multiplicative)
- CE2 Résoudre des problèmes additifs en une étape de types parties-tout et comparaison
- CE2 Résoudre des problèmes additifs en deux étapes
- CE2 Résoudre des problèmes multiplicatifs en une étape
- CE2 Résoudre des problèmes mixtes en deux ou trois étapes
- CE2 Résoudre des problèmes de comparaison multiplicative en une étape
- CE2 Résoudre des problèmes mettant en jeu des produits cartésiens
-
Grandeurs et mesures
- Les longueurs
24 objectifs
- CP Utiliser le lexique spécifique associé aux longueurs
- CP Comparer des objets selon leur longueur
- CP Comparer des segments selon leur longueur
- CP Savoir mesurer la longueur d'un segment en utilisant une règle graduée
- CP Connaitre et utiliser les unités mètre et centimètre et les symboles associés (m et cm)
- CP Connaitre quelques longueurs de référence
- CP Savoir qu'un mètre est égal à cent centimètres
- CE1 Connaitre et utiliser les unités mètre, centimètre, kilomètre et les symboles associés (m, cm et km)
- CE1 Choisir l'unité la mieux adaptée pour exprimer une longueur
- CE1 Connaitre les relations entre les unités de longueur usuelles
- CE1 Savoir mesurer la longueur d'un segment en utilisant une règle graduée
- CE1 Comparer des longueurs
- CE1 Connaitre quelques longueurs de référence
- CE1 Estimer la longueur d'un objet du quotidien
- CE2 Connaitre et utiliser les unités mètre, décimètre, centimètre, millimètre, kilomètre et les symboles associés (m, dm, cm, mm, km)
- CE2 Connaitre les relations entre les unités de longueur
- CE2 Choisir l'unité la mieux adaptée pour exprimer une longueur
- CE2 Comparer des longueurs
- CE2 Tracer un segment de longueur donnée
- CE2 Disposer de quelques longueurs de référence
- CE2 Estimer la longueur d'un objet ou une distance
- CE2 Savoir ce qu'est le périmètre d'une figure plane
- CE2 Comparer le périmètre de plusieurs polygones sans règle graduée, en utilisant un compas
- CE2 Déterminer le périmètre d'un polygone en utilisant une règle graduée
-
- Les masses
13 objectifs
- CP Utiliser le lexique associé aux masses
- CP Comparer des objets selon leur masse
- CE1 Savoir identifier l'objet le plus léger (ou le plus lourd) parmi deux ou trois objets de volumes proches en les soupesant ou en utilisant une balance pour les peser
- CE1 Connaitre et utiliser les unités gramme et kilogramme et les symboles associés (g, kg)
- CE1 Savoir que 1 kg est égal à 1 000 g
- CE1 Comparer des masses
- CE1 Disposer de quelques masses de référence. Estimer la masse d'objets du quotidien en gramme ou en kilogramme.
- CE2 Connaitre et utiliser les unités gramme, kilogramme et tonne et les symboles associés (g, kg, t)
- CE2 Choisir l'unité la mieux adaptée pour exprimer une masse
- CE2 Connaitre les relations entre les unités de masse usuelles
- CE2 Comparer des masses
- CE2 Disposer de quelques masses de référence
- CE2 Estimer la masse d'un objet
-
- Les contenances
3 objectifs
- CE2 Comparer les contenances de différents objets
- CE2 Connaitre et utiliser les unités litre, décilitre et centilitre et les symboles associés (L, dL et cL)
- CE2 Savoir que 1 L est égal à 10 dL et également à 100 cL
-
- La monnaie
14 objectifs
- CP Utiliser le lexique spécifique lié à la monnaie
- CP Comparer les valeurs de deux ensembles constitués de pièces de monnaie ou de deux ensembles constitués de pièces et de billets
- CP Déterminer la valeur en euro d'un ensemble constitué de pièces et de billets
- CP Constituer une somme d'argent donnée avec des pièces et des billets
- CP Simuler des achats en manipulant des pièces et des billets fictifs. Rendre la monnaie
- CE1 Connaitre le lien entre les euros et les centimes
- CE1 Comparer les valeurs en euro de deux ensembles constitués de pièces et de billets
- CE1 Déterminer la valeur en euro et centime d'euro d'un ensemble constitué de pièces et de billets
- CE1 Constituer avec des euros et des centimes d'euro une somme d'argent d'une valeur donnée
- CE1 Simuler des achats en manipulant des pièces et des billets fictifs. Rendre la monnaie
- CE1 Connaitre le sens de l'écriture à virgule d'une somme d'argent
- CE2 Simuler des achats en manipulant des pièces et des billets fictifs. Rendre la monnaie
- CE2 Poser et effectuer des additions de montants en euro
- CE2 Poser et effectuer des soustractions de montants en euro
-
- Le repérage dans le temps et les durées
12 objectifs
- CP Lire sur une horloge à aiguilles une heure donnée en heures entières
- CP Positionner les aiguilles d'une horloge correspondant à une heure donnée (uniquement des heures entières inférieures ou égales à douze)
- CP Associer une heure à un moment de la journée
- CE1 Lire l'heure sur une horloge à aiguilles (lorsque l'heure est donnée en heures entières, en heures et demi-heure ou en heures et quarts d'heure)
- CE1 Positionner les aiguilles d'une horloge correspondant à une heure donnée en heures entières, en heures et demi-heure ou en heures et quart d'heure
- CE1 Connaitre, utiliser et distinguer les heures du matin et celles de l'après-midi
- CE1 Connaitre les unités de mesure de durée, heure et minute, et les symboles associés (h et min)
- CE1 Comparer et mesurer des durées écoulées entre deux instants affichés sur une horloge (pour des intervalles de temps situés dans une même journée, avec des heures données en heures entières, en heures et demi-heure ou en heures et quarts d'heure)
- CE2 Lire l'heure sur une horloge à aiguilles
- CE2 Positionner les aiguilles d'une horloge correspondant à une heure donnée en heures entières ou en heures et minutes
- CE2 Comparer et mesurer des durées écoulées entre deux instants affichés sur une horloge (pour des intervalles de temps situés dans une même journée)
- CE2 Résoudre des problèmes à une ou deux étapes impliquant des durées
-
Espace et géométrie
- Les solides
15 objectifs
- CP Reconnaitre les solides usuels suivants: cube, boule, cône, cylindre, pavé
- CP Nommer un cube, un pavé et une boule
- CP Décrire un cube ou un pavé en utilisant le terme «face». Connaitre le nombre et la nature des faces d'un cube et d'un pavé.
- CP Construire des cubes et des pavés
- CE1 Reconnaitre les solides usuels suivants: cube, boule, cône, pyramide, cylindre, pavé
- CE1 Nommer un cube, une boule, un pavé, un cône ou une pyramide
- CE1 Décrire un cube, un pavé ou une pyramide en utilisant les termes «face», «sommet» et «arête»
- CE1 Connaitre le nombre et la nature des faces d'un cube ou d'un pavé
- CE1 Construire un cube, un pavé droit ou une pyramide
- CE2 Nommer un cube, une boule, un pavé, un cône, une pyramide ou un cylindre
- CE2 Décrire un cube, un pavé ou une pyramide en utilisant les termes «face», «sommet» et «arête»
- CE2 Connaitre le nombre et la nature des faces d'un cube ou d'un pavé
- CE2 Connaitre la nature des faces d'une pyramide
- CE2 Construire un cube, un pavé ou une pyramide
- CE2 Construire un cube à partir d'un patron
-
- La géométrie plane
21 objectifs
- CP Reconnaitre des formes planes (disque, carré, rectangle et triangle) dans un assemblage et dans son environnement proche
- CP Nommer le disque, le carré, le rectangle et le triangle
- CP Donner une première description du carré, du rectangle, du triangle en utilisant les termes «sommet» et «côté»
- CP Repérer visuellement des alignements
- CP Utiliser la règle pour repérer ou vérifier des alignements
- CP Utiliser la règle comme instrument de tracé
- CP Construire un carré, un rectangle, un triangle ou un assemblage de ces figures sur du papier quadrillé ou pointé
- CE1 Utiliser le vocabulaire géométrique approprié
- CE1 Reconnaitre, nommer et décrire un cercle, un carré, un rectangle, un triangle, un triangle rectangle en utilisant le vocabulaire approprié
- CE1 Connaitre les propriétés des angles et des égalités de longueur pour les carrés et les rectangles
- CE1 Reproduire ou construire un carré, un rectangle, un triangle, un triangle rectangle et un cercle ou un assemblage de ces figures
- CE1 Utiliser la règle pour vérifier des alignements et l'équerre pour vérifier qu'un angle est droit
- CE1 Utiliser la règle graduée, l'équerre et le compas comme instruments de tracé
- CE1 Connaitre et utiliser le code pour les angles droits
- CE2 Utiliser le vocabulaire géométrique approprié
- CE2 Reconnaitre, nommer et décrire le carré, le rectangle, le triangle, le triangle rectangle et le losange
- CE2 Connaitre les propriétés des angles et les égalités de longueur pour les carrés, les rectangles et les losanges
- CE2 Reproduire ou construire un carré, un rectangle, un triangle, un triangle rectangle et un cercle ou des assemblages de ces figures sur tout support (papier quadrillé ou pointé ou papier uni), avec une règle graduée, une équerre ou un compas
- CE2 Connaitre et utiliser le codage d'un angle droit et celui qui indique que des segments ont la même longueur
- CE2 Reconnaitre si une figure possède un ou plusieurs axes de symétrie en utilisant des pliages ou du papier calque
- CE2 Compléter, sur une feuille quadrillée ou pointée, une figure simple pour la rendre symétrique par rapport à un axe donné
-
- Le repérage dans l'espace
12 objectifs
- CP Connaitre et utiliser le vocabulaire lié aux positions relatives
- CP Situer des personnes ou des objets les uns par rapport aux autres ou par rapport à d'autres repères dans la classe
- CP Construire et utiliser des représentations de la classe pour localiser, mémoriser et communiquer un emplacement
- CP Construire et reproduire des assemblages de solides à partir d'un modèle en trois dimensions ou de représentations planes
- CP Se déplacer et décrire des déplacements dans la classe en s'orientant et en utilisant des repères
- CP Construire et utiliser un plan de la classe pour communiquer un déplacement
- CP Utiliser et produire une suite d'instructions qui codent un déplacement en utilisant un vocabulaire spatial précis
- CE1 Connaitre et utiliser le vocabulaire lié aux positions relatives
- CE1 Situer des personnes ou des objets les uns par rapport aux autres ou par rapport à d'autres repères dans un espace familier
- CE1 Construire et utiliser des représentations d'un espace familier pour localiser, mémoriser ou communiquer un emplacement
- CE1 Construire des assemblages de cubes et de pavés
- CE1 Comprendre, utiliser et produire une suite d'instructions qui codent un déplacement en utilisant un vocabulaire spatial précis
-
Organisation et gestion de données
- Collecte et organisation de données
7 objectifs
- CP Collecter des données et présenter ces données sous forme d'un tableau ou d'un diagramme en barres
- CP Construire et compléter un tableau à double entrée
- CE1 Produire un tableau ou un diagramme en barres pour présenter des données recueillies
- CE1 Lire et interpréter les données d'un diagramme en barres. Lire et interpréter les données d'un tableau à double entrée
- CE2 Produire un tableau ou un diagramme en barres pour présenter des données recueillies
- CE2 Lire et interpréter les données d'un tableau à double entrée ou d'un diagramme en barres
- CE2 Résoudre des problèmes en utilisant les données d'un tableau à double entrée ou d'un diagramme en barre
-
Exemples de programmations
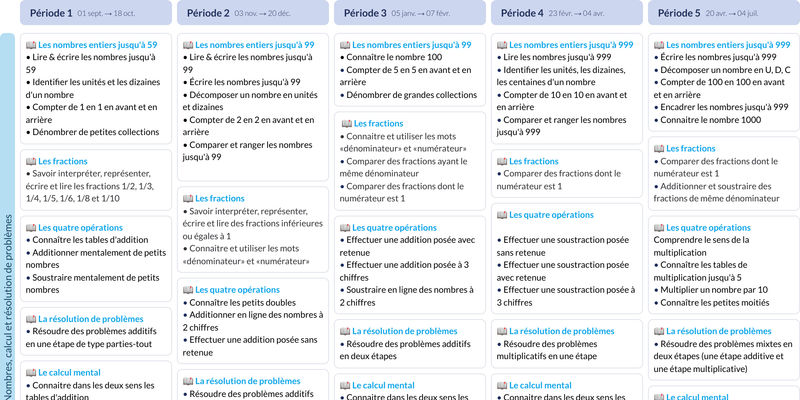
Programmation de Mathématiques par période pour CE1
Voici un exemple de programmation de mathématiques pour une classe simple de CE1. Elle est conforme aux programmes en vigueur et peut être mise en place quel que soit le manuel choisi.


Programmation Maths au CE1 (Accès)
Découvrez cette programmation de mathématiques issue du manuel "Maths au CE1" (Accès). Utilisez cette ressource telle quelle ou personnalisez-la en la modifiant directement en ligne sur Teetsh.


Programmation Les maths avec Méli CE1 (Le Livre Scolaire)
Découvrez cette programmation de mathématiques issue du manuel “Les maths avec Méli CE1” (Le Livre Scolaire). Utilisez cette ressource telle quelle ou personnalisez-la en la modifiant directement en ligne sur Teetsh.

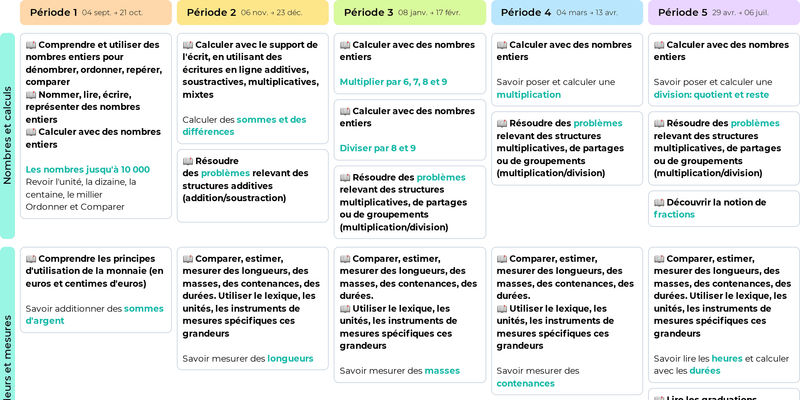
Programmation Mathématiques CE2 (basée sur La Méthode de Singapour)
Découvrez cette programmation de Mathématiques pour une classe de CE2. Utilisez cet exemple en le modifiant en ligne directement sur Teetsh.


Programmation MHM CE2
Voici la programmation annuelle MHM (Méthode heuristique Mathématiques) pour la classe de CE2.


Programmation Les maths avec Méli CE2 (Le Livre Scolaire)
Découvrez cette programmation de mathématiques issue du manuel “Les maths avec Méli CE2” (Le Livre Scolaire). Utilisez cette ressource telle quelle ou personnalisez-la en la modifiant directement en ligne sur Teetsh.
